Mulit-Armed Bandit (1)
본격적인 강화학습 알고리즘에 대한 공부에 앞서, Multi-armed Banit Problem에 대해 살펴보려 한다. MAB는 강화학습에 기초가 되는 컨셉이자, 한 분야이다. 최근들어 이를 잘 활용한 알고리즘들이 다양한 분야에서 응용되고 각광받고 있다.
대표적인 예로, Netflix에서 사용하는 추천시스템 알고리즘 또한 MAB를 활용한 알고리즘 이다.
What is Multi-armed Banit?
Multi-armed bandit은 슬롯머신 게임에서 유래된 말이다.
여러 개의 슬롯머신을 플레이한다고 해보자. 누구나 슬롯머신을 통해 최대한 많은 돈을 따고 싶을 것이다. 그러나, 우린 시간과 돈이 한정되어 있기에 잭팟이 터질 때까지 계속 플레이할 순 없다. 그렇다면, 효율적으로 최대의 돈을 딸 수 있는 방법은 무엇일까?
이에 대해 생각해보기 위해선 두가지를 고려해야한다.
- 돈을 딸 확률이 높은 슬롯머신인가?
- 아직 어떤지 모르는 슬롯머신인가?
만약 기존 경험을 바탕으로 돈을 딸 확률이 높은 슬롯 머신만 공약한다면, 실제로 더 좋은 기회를 놓칠 수도 있고, 불확실성이 높은 슬롯 머신을 계속해서 탐색한다면, 탐색만 하다가 탕진할 수도 있다.
직관적으로도 느껴지겠지만 위에서 말한 탐색(exploration)과 이용(exploitation)은 Trade-Off관계에 있다. 따라서, exploration과 exploitation을 적절한 비율로 활용하여 최적의 값을 찾아내는 것이 가장 중요하다. 이것이 바로 Multi-armed Banit Problem의 핵심이다.
오늘은 MAB를 활용한 가장 대표적인 알고리즘 3가지에 대해 소개할 것이다. 이에 대한 advanced algorithm들은 다음 포스팅에 쓰도록 하겠다.
MAB Algoritm의 목표는 주어진 n개의 행동과 t번의 시간 안에서 Reward를 최대화하는 것이다. 즉, 다음과 같은 Loss function(=Regret function)을 최소화 하는 것이 목표이다.
\[R = \left(\max_{i=1,\ldots,K} \mathbb E \sum_{t=1}^H x_{i,t}\right) - \mathbb E \sum_{t=1}^H x_{S_t,t}\]
위 식은 Optimal하게 플레이 했을 때의 reward와 현재 시점에서의 실제 reward의 차이를 보여준다. 최적의 값과 가장 비슷한 값을 찾는다는 논리는 현실적이면서도 꽤 그럴듯하다.
그러나, 안타깝게도 실제 문제에선 모든 시점의 Reward를 다 알 수 없으며, regret function도 정확히 구하긴 매우 어렵다. 따라서, 실제론 보상에 대한 Prior 분포를 할당하거나 Loss function을 사용하지 않고 최적의 값을 찾는 방법들을 주로 사용한다.
Epsilon-greedy Algorithm
\(\epsilon\)-greedy algorithm은 가장 간단하면서도 대중적인 알고리즘이다.
(1-\(\epsilon\))의 확률로 지금 시점t까지의 관측값 중 가장 reward가 큰 점을 action을 고르고, \(\epsilon\)의 확률로 나머지 action들 중 랜덤하기 고른다. 이때, \(\epsilon\)은 exploration과 exploitation의 비율을 조절하는 hyper-parameter의 역할을 한다.

이 알고리즘은 성능이 연산이 적어 빠르고, 직관적이라는 장점이 있다. 그러나, constant한 \(\epsilon\)이 적절하지 못하면 불필요한 탐색을 하거나, 충분한 참색이 이루어지지 않을 수도 있다는 문제가 있다.
Upper Confidence Bound
실제로 매 시간마다 action에서 얻는 보상은 변하지 않는 값이 아닌 random variable이기 때문에 지금 순간에 empirical mean이 크다고해서 정말로 해당 action이 최적의 선택이라고 할 수는 없다. 이와 같은 문제를 보완하고자 만든 알고리즘이 Upper Confidence Bound이다.
Upper Confidence Bound 알고리즘은 epsilon-greedy 알고리즘에 비해 성능이 뛰어나며, 최근까지 가장 많이 사용되는 알고리즘이다. UCP 알고리즘은 기존 trade-off의 비율을 조절하는 hyper-parameter가 constant하다는 관점과 달리, 이를 시간 t에 따라 변하는 확률값으로 바라본다.
조금 더 쉽게 말하자면, 기존 관측값(empirical mean)의 사용에 비해 새로운 탐색값을 사용하는 비중을 시간t와 action i에 따라 다르게 준다.
\[i=argmax_i[Q_{ti}+P_i]\]
여기서 \(Q_{ti}\)는 t시간에 i의 empirial mean을 의미하고, Pi는 action i의 불확실성에 대한 확률값이다. Q는 exploitation, P는 exploration하는 식으로 이해하면 된다. 이때, Pa값은 다양하게 정의가능하며, 이에 따라 UCB는 다양한 방법으로 존재한다. ex) UCB1, bayes-UCB, KL-UCB,,,
이론적으로는 더 좋은 UCB를 사용할 수록, Regret function의 값이 작아진다.
1) UCB1
\[argmax_i[Q_t+c\sqrt{\frac{log\,t}{N_t(a)}}]\]
Upper Confidence Bound1은 Pi를 정의하는 가장 간단한 방법론이다. 이때 N_t는 현재 시간에서 action a가 선택된 횟수를 의미한다. 위 식을 해석해 보자면, 관측치가 많지 않을 땐 관측결과를 기준으로 고르되, 시간이 지나고 나면 경험적 결과에 더 큰 가중치를 두게 된다. (time은 log scale이지만 관측은 linear scale이므로)
위 UCB1공식은 Hoeffding’s Inequality를 사용하여 유도 가능하다.
\[P[E[X]>\bar{X_t}+P_{ti}]\leq e^{-2N_{ti}P_{ti}^2}\]
2) Bayes-UCB
Bayes-UCB에선 reward에 대한 Prior \(p[R]\)를 설정한다. 이를 통해 reward의 기대값에 대한 posterior \(p[R|h_t]\)를 찾는다. 이때, 시간과 관련된 term에 대해 UCB로 삼는다.
\[argmax_iQ(1-\frac{1}{t},\lambda_i^{t-1})\]
이때, Q함수는 확률분포를 quantile로 변환하는 함수로, \(P_\rho (X\leq Q(t,\rho ))=t\)를 만족하는 값이다.
Thompson Sampling
Thompson Sampling(=Probability Matching)은 비교적 최근 만들어진 알고리즘으로 MAB문제에서 상당히 좋은 성능을 낸다고 알려져 있다. 이 알고리즘의 핵심 컨셉은 각 Reward의 Parameter를 하나의 random variable로 보고, 해당 분포로부터 random sampling한다는 것이다. 이렇게 Sampling한 값들 중 reward의 기댓값이 가장 큰 action을 선택하고, 이를 반영하여 다시 Parameter의 분포를 update한다.
Parameter에 분포를 할당하여 MAP(Maximum a Posteriori) 문제를 푼다는 컨셉으로 본다면 Thompson Sampling은 Bayesian UCB의 한 갈래로도 말할 수 있다.
Thompson sampling에서의 MAP 값은 다음과 같다.
\[max_\theta Pr[\theta|D]=\prod Pr[r_t|a_t,x_t,\theta]Pr[\theta]\]
보통 우리는 random variable로 표현된 Reward를 Maximize하는 값을 목표로 두고 있기에, 위 식을 Reward에 대한 식으로 변형할 수 있다.
\[E[r|a]=\int E[r|a,\theta]Pr[\theta|D]d\theta\]
설명을 간편하게 하기 위해, Reward가 있다(1), 없다(0)의 형태로만 존재한다고 가정하자. Reward의 분포는 다음과 같이 나타낼 수 있다.
\[Bernoulli(x|\theta)=\begin{cases} & \theta \;\;\;\;\;\;\;\;\text{ if } x=1 \\ & 1-\theta \;\;\text{ if } x=0 \end{cases}\]
그렇다면, Reward의 Parameter \(\hat{\theta}\)의 Prior로 \(Beta(\alpha_k,\beta_k)\)를 할당할 수 있다. Beta-Bernoulli 분포의 Conjugate한 성질로 인해, reward를 관찰한 후 \(\alpha_k\)와\(\beta_k\)의 값은 다음과 같이 업데이트 된다.
\[(\alpha_k,\beta_k)=\begin{cases} &(\alpha_k,\beta_k)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{ if } x_t=k \\ & (\alpha_k+r,\beta_k+1-r)\;\text{ if } x\neq k \end{cases}\]
Parameter가 \((\alpha,\beta)\)일 때의 Beta분포의 분산은 \(\frac{\alpha \beta }{(\alpha+\beta )^2(\alpha +\beta +1)}\)이다. 우리가 주의깊게 봐야할 것은 \(\alpha+\beta\)가 커질 수록 분산은 작아지게 된다는 점이다. 이 알고리즘에선 관찰값이 많을 수록 \(\alpha + \beta\)가 커지게 되므로, 확률분포의 형태가 점점 뾰족해지게 된다. 즉, 시간이 지날 수록 관측값이 reward가 높은 점으로 수렴해간다고 볼 수 있다.

알고리즘에 대한 간략한 예시는 여기를 참고하자.
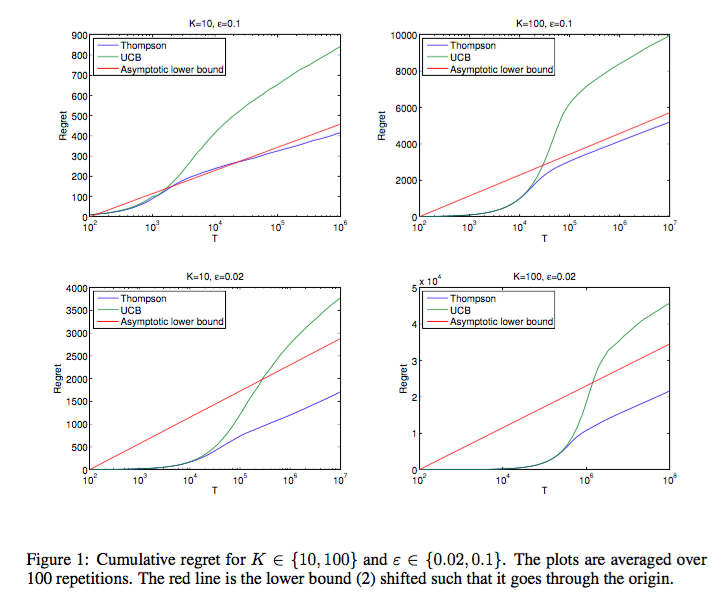
기본 아이디어도 어렵지 않고, 알고리즘 또한 엄청나게 간단한 편임에도 Thompson sampling은 다음 그래프에서 볼 수 있듯 UCB 등의 기존 알고리즘보다도 더 좋은 performance를 내는 것을 알 수 있다.
References
https://github.com/bgalbraith/bandits
http://sanghyukchun.github.io/96/
http://web.stanford.edu/class/cs234/CS234Win2019/slides/lecture12_postclass.pdf
