Multi-Armed Bandit(3)
지난 포스팅에선, Non-stationary Bandits 중 Non statioary Stochastic bandits, 구체적으로 Dynamic Thompson Sampling과 Discounted Thompson Sampling을 공부하였다. 이어서 오늘은 Contextual Bandits에 대해 포스팅하려한다.
-
Multi-Armed Bandits: 보상을 최대화하는 machine를 찾기 위해, 적절한 action을 통해 Exploration과 Exploitation를 찾아가는 문제를 말한다. 대부분의 경우 Stochastic bandits의 형태이다. MDP와 함께 강화 학습의 큰 축 중 하나이다.
-
Non-stationary Bandits: 보상에 대한 분포가 일정하다는 가정이 존재하지 않는다. (이 분포는 대게 환경에 따라 변화하는데, 여기서 환경이란 대부분 시간이나 Agent에 대한 정보를 의미한다.) 따라서, 모든 파라미터들은 확률변수로 존재하며, 모든 시간에서의 최선의 옵션이란 존재하지 않는다.
- Adversarial bandits
- Stochastic bandits
- Contextual bandts
Non-stationary bandits의 종류를 나누는 것에는 애매한 사항이 있다. 특히, Contextual bandit은 Adversarial bandit 혹은 Stochastic bandit과 배타적이지 않다. 다시 말해, Stochastic한 관점에서 Contextual bandit을 바라보거나 Adversarial의 관점에서 Contextual bandit을 바라보는 알고리즘이 존재한다.
What is Contextual Bandit?
Contextual Bandits은 포털사이트 “Yahoo”에서 메인화면 최적화 알고리즘으로 잘 알려져있다. 뿐만 아니라, 넷플릭스와 같이 초개인화 추천서비스가 필요한 곳에서도 사용되고 있다.
알고리즘에 대해 설명하기 앞서 쉬운 예제를 하나 들어보자.
넷플릭스에서 개개인에 맞는 영화를 추천하고자 한다. 가장 간단한 방법은 한 사람이 그동안 시청한 과거 기록을 바탕으로 추천하는 것이다. 이 것이 Stationary MAB의 개념이다. 그러나, 이것만으로는 조금 부족하다. 그 사람이 가입 당시 입력한 즐겨보는 장르, 프로필도 영상 선택에 영향을 줄 수 있지 않을까? 뿐만 아니라, 현재 사회/문화적 이슈도 영향을 줄 수 있을 것이다. (현재 COVID-19로 인해 재난 영화가 급부상하는 것 처럼 말이다.)
이렇게 과거 경험뿐만 아니라, 사용자를 둘러싼 환경적인 요소도 예측에 이용한다면, 조금 더 정확한 추천이 될 것이다. 이것이 Contextual Bandits의 메인 아이디어이다.
그렇다면, 다른 Non-stationary Bandits과는 어떤 점이 다를까?
State 개념의 추가
- 기존 MAB문제에선 Agent가 특정 행동을 하면, 이것에 대한 보상이 주어졌다.
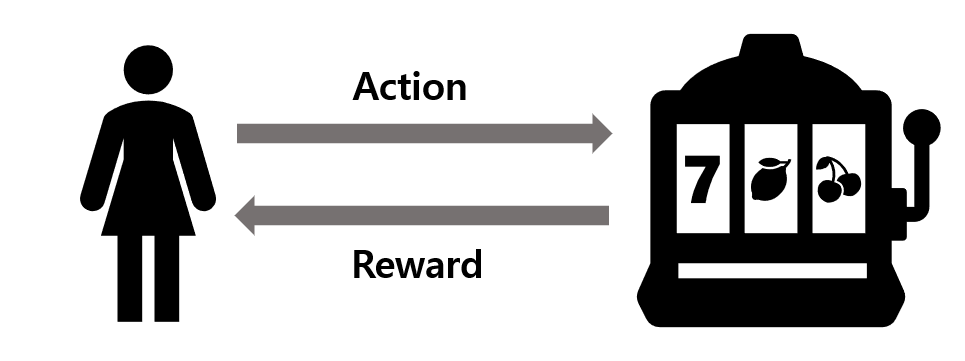
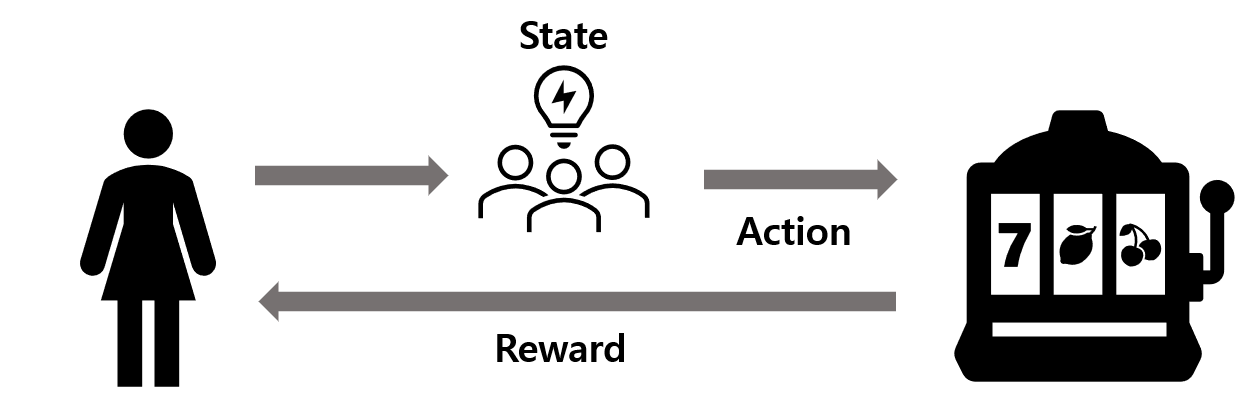
- 그러나, Contextual bandits 문제는 State의 개념을 추가한다.
- 여기서의 State란 위 예제에서의 사용자를 둘러싼 환경이라 볼 수 있다.
- 아래 그림에서와 같이, Agent는 행동을 취하기 전에 State를 관측하여 이를 의사결정에 반영한다.
- 즉, Action에 따라 State가 변하지 않는다.
Policy 개념의 추가
-
Contextual bandits문제는 State 개념이 추가되었기 때문에, 이에 따라 Policy의 개념도 사용한다.
- Matching from Contexts to arms
[주의]
- (Action, State, Reward)의 개념은 Markov Decision Process에서도 많이 사용되는 개념이다. 그러나, Contextual Bandits에서의 State개념과 MDP의 State개념은 다르다.
- Contextual Bandits에서의 State는 Action에 따라 변화하지 않지만, MDP에서의 State는 Action에 따라 변화한다.
-
Policy의 개념 또한 MDP와 Contextual Bandit에서 각각 다르게 사용된다.
-
Contextual Bandit: Matching from Contexts to arms
-
MDP: Matching from state to action
-
그럼에도 불구하고, Contextual bandits은 고전적으로 사용하는 MDP Reinforcement Learning의 원리와 거의 유사하여, MAB문제의 확장판이자, 강화학습의 축소 형태라 불린다.
Notation
\(K\): Number of arms
\(T\): Total number of time steps
\(C\): The set of contexts
\(\pi\): \(C \rightarrow [K]\): A policy
\(\Pi\): The class of all of policies
\(a_t\) or \(I_t\): The arm choosen at time t
\(r_t\): The reward received at time t
\(l_{i,t}\): The loss incurred by pulling arm i at time t
Problem Setting
- Observe context \(x_t \in C\) (randomly chosen)
- Choose arm \(I_t \in [K]\) (action taken by the algorithm)
- Receive a reward \(r_t\) or equivalently, \(l_{i,t}\)
- Update the data set with {\((r_t,x_t,I_t)\)}
Off-Policy Evaluation
강화학습에서 중요한 것 중 하나는 각 Policy의 성능(대부분은 보상의 크기)을 잘 평가하는 것이다.
실제 데이터는 우리가 Simulation할 수 없는, logged data인 경우가 많다. 즉, 우리가 관심있지만 관측할 수 없는 Policy가 존재할 수 있다. 혹은 관측되었다 하더라도, random policy에 따라 선정되었을 가능성이 높다.
이때 우리가 원하는 Policy \(\pi_t\)의 성능을 어떻게 평가할 수 있을까?
- 우선, 다음과 같은 가정이 필요하다.
- \(\forall x,a\;:\;if\;\pi(a \mid x)>0,\;then\; p(a \mid x)>0 \)
- 우리의 목표는 i.i.d samples \({(x_s,a_s,r_s)}_{s=1}^{n}\)하에서, 우리가 알고 싶은 \(\pi(x_s)\)의 expected reward를 구하는 것이다.
- 즉, \(R^*(x,\pi(x))=\frac{1}{n}\sum_{s=1}^{n}E_{r\sim P(. \mid x_s,\pi(x_s))}[r]\) 를 구하고자 한다.
- 이 문제는, fixed \(x,a\)에 대하여 \(R^*(x,a)\)를 구할 수 있다면 쉽게 풀 수 있다.
-
Inverse Propensity Score estimator를 활용하면, \(R^*(x,a)\)의 unbiased estimator를 쉽게 구할 수 있다.
-
\(\hat{R}(x_s,a)=r_s\frac{I_{a_s=a}}{p(a_s \mid x_s)}\)
-
주어진 state \(x_s\)에서 \(a_s\)가 선정될 확률의 역수가 곱해진다. 이는 선정 확률 \(p(a_s \mid x_s)\)이 작지만 보상 \(r_s\)가 큰 경우에 가중치를 두어 sampling bias를 보정하는 역할을 한다.
아직 완벽히 이해하진 못했다. 이 통계 기법에 대해 조금 더 공부 해봐야할 것 같다.
-
Algorithms
이번 포스팅에선 EXP4 알고리즘을 위주로 설명할 예정이다. 이외에 다른 여러 알고리즘이 궁금하다면 [1]을 참고하길 추천한다.
C-EXP3과 EXP4알고리즘의 경우 Adversarial Contextual Bandit 알고리즘의 일종이다. Adversarial Bandit의 관점은 “적군에 있는 사람이 나의 행동에 대한 Reward function을 조정한다.”라고 이해할 수 있다. 조금 더 일반화한다면, Reward가 Random하게 주어진다고 봐도 무방하다. Reward가 random하기 때문에 많은 실제 사회의 문제에 적용가능하다는 장점이 있지만, 반대로 정확한 Reward나 Regret의 최적값을 찾기 어렵다. 따라서, Adversarial Bandits 알고리즘의 성능은 대게 Regret bound를 통해 평가한다.
C-EXP3 Algorithm
(Exponential-weighted algorithm for Exploration and Exploitation)
-
우선 하나의 context엔 한개의 bandit만 존재하는 단순한 케이스를 먼저 생각해보자. 이러한 경우, 각 context는 모두 i.i.d하다는 가정을 할 수 있다. 따라서, “처음에 Context에 대한 정보를 추가적으로 반영한다는 점”을 제외하곤 기존 MAB와 동일하다.
- Pseudo-Regret: \(\bar{R_T}= max_{\pi}E[\sum_{t=1}^{T}l_{I_t,t} - \sum_{t=1}^{T}l_{\pi(x_t),t}]\)
-
Regret bound for \(C\)-EXP3: \(\bar{R}_T\leq \sqrt{2T \mid C \mid KlnK}\)
- 그러나 관찰가능한 context가 많아지면, EXP3알고리즘은 다음과 같은 한계점을 지닌다.
- 각 context에 대한 데이터가 너무 적다.
- 모든 context를 완전한 독립 관계로 보기 때문에, 계산량이 많다.
EXP4 Algorithm
(Exponential-weighted algorithm for Exploration and Exploitation with Experts)
-
C-EXP3 Algorithm의 한계를 보안하여 만들어진 알고리즘이다.
-
이 알고리즘에선 모든 context가 독립이란 가정을 하지 않는다.
-
대신 expert라는 개념을 도입한다. 여기서의 expert란 Context를 표현하기 위한 장치로, 유사한 context의 특성들을 묶어준다.
- 예를 들어 보험 가격을 예측을 하고자 한다면, 개인의 context는 (나이, 기저질환, 과거 병력)등이 있을 것이다. 이때, 각 “나이”, “기저질환”등은 experts가 되어 개인의 특징을 보여준다.
위 알고리즘을 내가 이해한대로 아래에 정리하였다.
1. 우선 언급되는 여러 확률분포에 대해 정리를 해보자.
- Experts의 확률분포: \(q_{1,t}=Uniform\){\(1,2,…,K\)}
- \(q_{i,t}\)의 분포는 time step마다 업데이트된다.
-
arms의 확률분포: \(\xi_{k,t}\)
- \(k^{th}\) expert에서의 arm에 대한 확률분포이기 때문에, experts advice라고도 한다.
- can be any probability distribution over the \(K\) arms.
-
EXP4에선 위 두 확률분포를 모두 사용한다.
- \(p_t=E_{k\sim q_t}[\xi_{k,t}]\)
2. 위 확률변수 \(p_t\)를 통해 arm \(I_t\)를 결정한다.
3. 선택된 \(I_t\)를 바탕으로 loss function을 구한다.
-
\(arm_i\)의 loss function \(l_{i,t}\)를 구한다.
- 이때, 앞서 언급한 Inverse Propensity Score trick을 사용한다.
-
\(expert_k\)의 loss function \(y_{k,t}\)를 구한다.
- \(y_{k,t}=E_{i\sim \xi_{k,t}}[l_{i,t}]\)
4. expert의 확률분포 \(q_{t+1}\)을 업데이트한다.
Conclusion
- 위 표와 같이 오늘 다룬 Exp4외에도 다양한 알고리즘들이 Contextual Bandit에 사용된다.
- 특히, LinUCB 알고리즘은 추가적으로 공부하면 좋을 것 같다.
[개인적인 의견]
-
만약 분류 예측값에 명확한 기준이 있다면, 우린 굳이 이 Contextual Bandits을 사용할 필요가 없다.
- ex) 광고를 클릭한다, 구매를 3번 이상 한다.
- tree기반의 ensemble 모형으로도 충분히 좋은 성능을 낼 수 있다.
-
그러나, 현실에선 예측값에 대한 명확한 기준이 없거나 그저 “다다익선”인 경우가 훨씬 많다.
- ex) 광고를 최대한 많이 클릭하게 만드는 방법
- 일반 Supervised Learning으론 예측이 어렵다.
-
후자의 경우 Contextual Bandits을 사용하면, 하나의 모델로 개개인에 맞는 예측(혹은 추천)이 가능하다는 장점과 더불어, 명확한 Y변수 없이도 학습이 가능하다.
- 더 나아가 Online Learning이 용이하다는 장점도 있다.
앞으론 더 꼼꼼히 공부해봐야지.
References
Lecture10: Contextual bandits
The Epoch-Greedy Algorithm for Multi-armed Bandits with Side Information


