Bayesian Optimization
Hyperparameter Tuning
모델을 만들어 적합시킬 때, 모델의 Structure만큼이나 모델의 성능을 좌우하는 것이 Hyperparameter입니다.
Hyperparameter란 주변수가 아닌 모델에서 자동 설정되는 변수로, learning rate이 그 대표적인 예입니다.
‘tree기반의 ensemble model’등 많이 사용하는 머신러닝 알고리즘들은 대부분 hyperparameter에 굉장히 예민하기 때문에, 이를 잘 조정하는 것이 매우 중요합니다.
따라서 오늘은 이 hyperparameter를 최적화하는 방법에 대해 다뤄보고자 합니다. 그 중에서도, 베이지안 컨셉을 적용한 Bayesian Optimization을 중점적으로 다룰 예정입니다.
우선 hyperparameter tuning의 여러 방법들에 대해 살펴봅시다. 모든 방법은 쉽게 말해 hyperparameter에 특정 값들을 대입하여 모델의 성능을 비교해본 후, 가장 높은 성능일 때의 hyperparameter를 찾는 과정이라 볼 수 있습니다. 그러나 naive하게 이 과정을 시행한다면 (가능한 모든 값을 대입해 본다면), 시간적 한계에 부딪히게 됩니다. 따라서, 모든 최적화 방법의 주요 요점은 얼마나 효율적으로 최적화 값을 찾아내는가라고 할 수 있습니다.
Grid Search
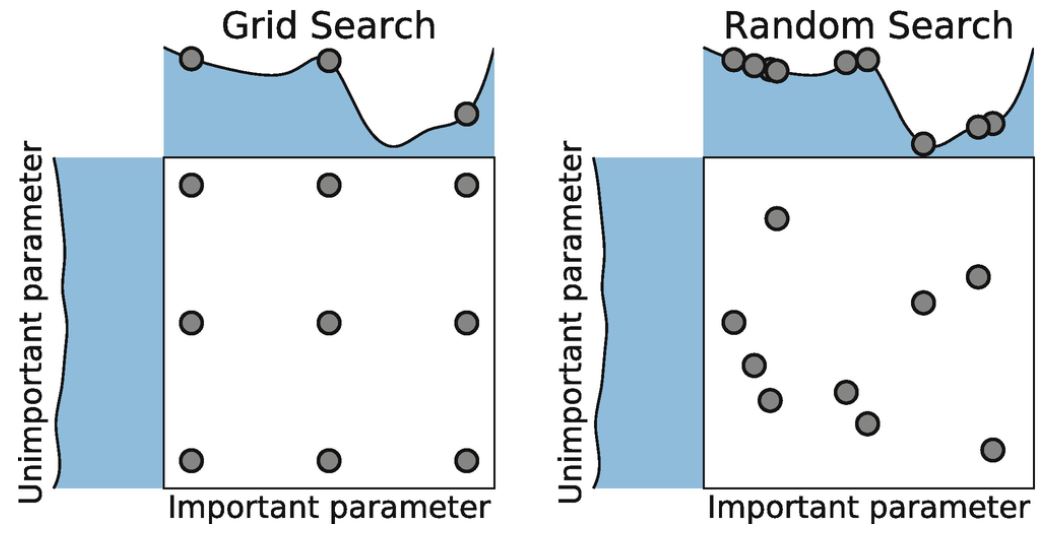
Grid Search는 사용자가 설정한 특정 구간 내에서 특정 간격으로 최적값을 탐색하는 방법입니다.
최적값에 대해 비교적 균등하고 전역적인 탐색이 가능하다는 장점이 있으나, 사용자가 설정한 값에 따라 Global Optima가 아닌 값이 산출될 수도 있으며 시간이 많이 소요된다는 단점 존재합니다.
Random Search
Random Search는 사용자가 설정한 특정 구간 내에서 Random하게 최적값을 탐색하는 방법입니다. Grid Search보단 시간 효율성이 높다는 장점이 있습니다.
- 이해를 돕기 위해 두 방법론에 대한 이미지를 첨부합니다. 출처
그러나, 이 두 방법은 t번 째 탐색에서 t-1번 째까지의 정보를 전혀 반영하지 않는 문제가 있습니다. 만약, t-1까지의 사전 정보를 가지고 t번 째 어느 값을 탐색할 지 결정할 수 있다면 훨씬 효율적일 것 같다는 생각이 듭니다.
Bayesian Optimization
위에서 언급한, 사전 정보를 최적값 탐색에 반영하는 것이 바로 Bayesian Optimization의 핵심 컨셉입니다. 이는 Bayesian Statistics의 기본 아이디어라고도 할 수 있는데 이부분은 추후에 따로 포스팅하도록 하겠습니다.
Bayesian Optimization에서 사전정보를 바탕으로 탐색하기 위해선 다음과 같은 정보가 필요합니다.
- 어떻게 모델 내에서 사전정보를 학습하고 자동적으로 업데이트할까?
- 수집한 사전정보를 바탕으로 어떤 기준으로 다음 탐색값을 찾을까?
Surrogate Model
첫번째 물음에 대한 답이 바로 Surrogate Model입니다.
정의를 살펴보자면, 기존 입력값 \((x_1,f(x_1)),…,(x_t,f(x_t))\)들을 바탕으로 미지의 목적함수 \(f\)의 형태에 대한 확률적인 추정을 하는 모델입니다. 일반적으로는 Surrogate Model로 Gaussian Process를 사용합니다. 참고 \[ f(x)∼GP(μ(x),k(x,x′))\]
Acquisition Function
두번째 물음에 대한 답은 Accuisition Function을 통해 찾을 수 있습니다. Surrogate Model이 목적 함수에 대해 확률적으로 추정한 결과를 바탕으로, 바로 다음 번에 탐색할 입력값 후보를 추천해 주는 함수라고 정의합니다.
추천에는 보통 두가지 기준이 있습니다. 직관적으로 생각해보면 쉽게 이해할 수 있습니다.
- 최적화 값일 가능성이 높은 값 = Surrogate Model에서 함수값이 큰 값
- 아직 Surrogate Model에서의 추정이 불확실한 값 = Surrogate Model에서 표준편차 \(\sigma(x)\)가 큰 값
지금까지의 정보를 바탕으로 최선의 선택이었던 값, 아직 불확실해서 확인해볼 필요가 있는 값 모두 그럴듯하며 탐색할 가치가 있어보입니다.그러나, 아쉽게도 이 두 전략은 Trade-Off관계입니다. 따라서, 실제 Acquisition Function을 짤 때는 이 두 전략을 적절히 반영하도록 하는 것이 중요합니다.
Expected Improvement
Expected Improvement(EI)함수는 위 두가지 전략을 일정수준 모두 포함하도록 설계된 함수로, Acquisition Function으로 가장 많이 사용됩니다.
현재까지 조사된 점들의 함숫값 \(f(x_1),…,f(x_t)\) 중 최대 함숫값 \(max_if(x_i)\)보다 더 큰 함숫값을 도출할 확률(PI) 및 그 함숫값과 \(max_if(x_i)\) 간의 차이값을 종합적으로 고려하여, 해당 입력값 \(x\)의 유용성을 나타내는 숫자를 출력합니다. 지금까지 나온 값보다 더 좋은 값이 나올 확률과 그렇다면 그 값이 얼마나 좋은 값일지를 모두 고려한다고 보면 됩니다.
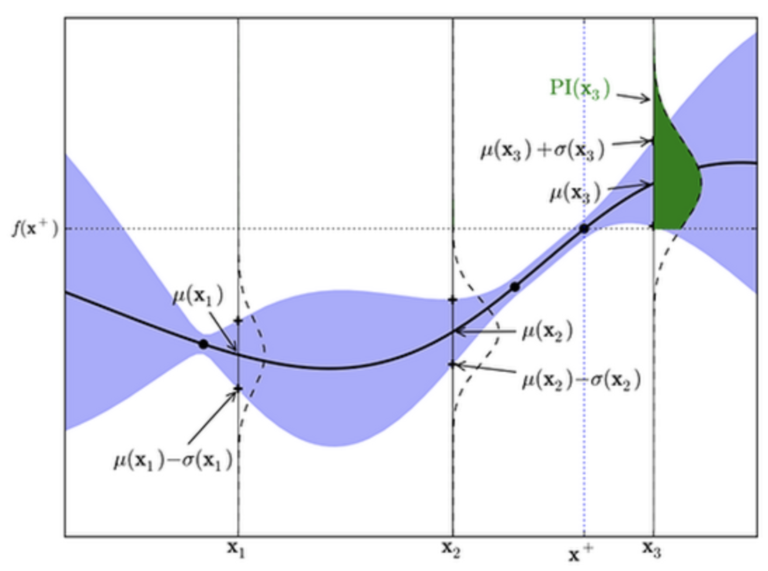
그림을 보면, 지금까지 관찰된 값 중 가장 함수값이 큰 점은 \((x_+,f(x_+))\)입니다. 이 때, 더 오른쪽의 후보값 \(x_3\)에 대한 \(f(x_3)\)의 확률추정 결과는 세로로 그려진 가우시안 분포를 따르게 됩니다.
분포를 보면 \(f(x_+)\)보다 위쪽인 영역(녹색)이 큰 것을 볼 수 있습니다. 이는 \(f(x_3)\)이 \(f(x_+)\)보다 클 확률이 높다는 것을 의미하고, \(x_3\)가 유용하다는 결론으로 이어지게 됩니다. 이렇게 계산한 PI 값에, 함숫값 \(f(x3)\)에 대한 평균 \(μ(x3)\)과 \(f(x_+)\) 간의 차이값만큼을 가중하여, \(x_3\)에 대한 EI 값을 최종적으로 계산합니다.
Gaussian Process를 사용한 EI에 대한 식은 다음과 같습니다. (유도과정)
\[\begin{align} EI(x) & = \mathbb{E} [\max (f(x) - f(x^{+}), 0)] \\ & = \begin{cases} (\mu(\boldsymbol{x}) - f(\boldsymbol{x}^{+})-\xi)\Phi(Z) + \sigma(\boldsymbol{x})\phi(Z) & \text{if}\ \sigma(\boldsymbol{x}) > 0 \\ 0 & \text{if}\ \sigma(\boldsymbol{x}) = 0 \end{cases} \end{align}\] \[Z = \begin{cases} \frac{\mu(\boldsymbol{x})-f(\boldsymbol{x}^{+})-\xi}{\sigma(\boldsymbol{x})} & \text{if}\ \sigma(\boldsymbol{x}) > 0 \\ 0 & \text{if}\ \sigma(\boldsymbol{x}) = 0 \end{cases}\]위 식에서 \(Φ와 ϕ\)는 각각 표준정규분포의 CDF와 PDF를 나타내며, ξ는 위에서 언급한 Acquisition Function의 두가지 기준 간 상대적 강도를 조절해 주는 파라미터입니다. ξ를 크게 잡을수록 두번째 기준의 강도가 높아집니다.
작동방법
그럼 이제 Bayesian Optimization이 어떻게 작동하는지 알아봅시다.
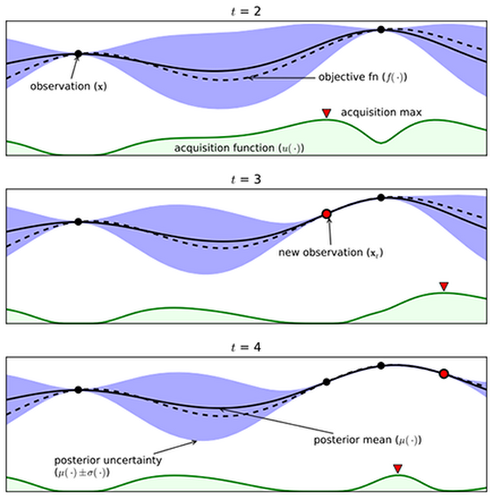
그림에서 검은 점선은 실제 목적함수, 검은 실선은 우리가 추정한 목적함수(Surrogate Model)를 말합니다. 또한, 파란 영역은 추정된 \(\sigma(x)\), 하단 녹색 실선은 Acquisition function을 보여줍니다.
- t=2일 때의 Acquisition Function이 최대화 되는 값은 t=3 시점에서 새로 관찰할 점으로 들어가게 됩니다.
- 이에 따라, t=3에서 새로 관찰한 함수값 주변의 파란 영역(\(\sigma\))이 크게 줄어들며, 동시에 acquisition function 또한 Update됩니다.
- 마찬가지로 t=3의 acquisition function이 Max가 된 지점에서 t=4의 새로운 관찰값이 생성되고, 그 주변의 파란 영역(\(\sigma\))이 줄어들며 acquisition function이 다시 update됩니다.
- EI의 정의에 따라 \(\sigma\)의 영역(불확실성)이 큰 부분과 함수값이 큰 부분에서 Acquision function이 높게 나타남을 확인할 수 있습니다.
- 이러한 과정이 계속 반복되면서 estimation값이 실제 목적함수에 근사하게 되고, 근사한 함수에서 최종 최적화값을 찾을 수 있습니다.
CODE
- Bayesian Optimization의 Python Code를 첨부합니다.
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from bayes_opt import BayesianOptimization
from bayes_opt.util import Colours
def dtc_cv(max_depth, min_samples_split,min_samples_leaf, max_features, data, targets):
estimator = DecisionTreeClassifier(
max_depth=max_depth, #여기에 원하는
min_samples_split=min_samples_split, #파라미터 넣고
min_samples_leaf=min_samples_leaf,
max_features=max_features, #값 넣지 말고 그냥 이름만
random_state=1
)
cval = cross_val_score(estimator, data, targets,
scoring='neg_log_loss', cv=5)
return cval.mean()
def optimize_dtc(data, targets):
def dtc_crossval(max_depth, min_samples_split,min_samples_leaf, max_features):
return dtc_cv(
max_depth=int(max_depth), #여기도 수정
min_samples_split=int(min_samples_split),
min_samples_leaf= int(min_samples_leaf) #여기
max_features=int(max_features), #여기
data=data,
targets=targets,
)
optimizer = BayesianOptimization(
f=dtc_crossval,
pbounds={
"max_depth": (1,30)
"n_estimators": (1,30), #여기 파라미터들 범위
"min_samples_split": (2, 25),
'min_samples_leaf':(1,30), # 넣어주기
"max_features": (1,20),
},
random_state=1234,
verbose=2
)
optimizer.maximize(n_iter=10)
print("Final result:", optimizer.max)
optimize_dtc(X_train, y_train)
Reference
http://www.juyang.co/how-exactly-does-bayesian-optimization-work/
http://research.sualab.com/introduction/practice/2019/02/19/bayesian-optimization-overview-1.html