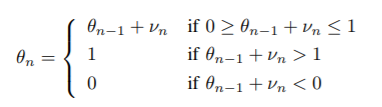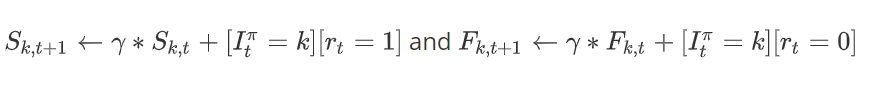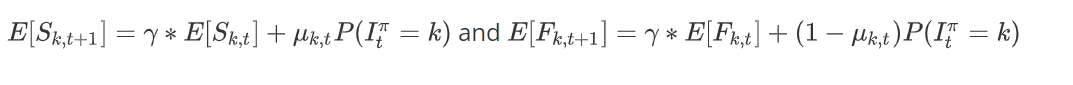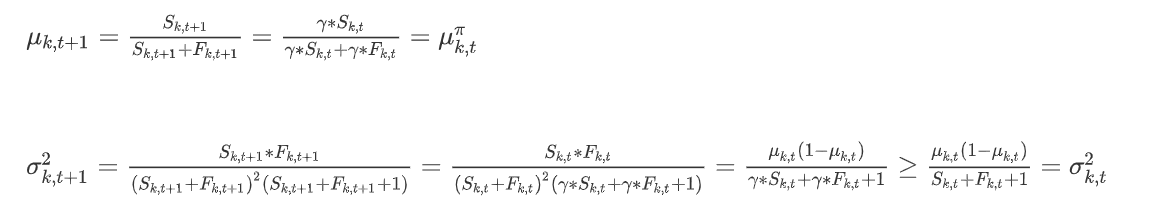Mulit-Armed Bandit(2)
지난 포스팅에선 Multi-armed Bandits 중 Stationary bandits Problem을 공부하였다. 대부분의 고전적인 MAB algorithm들은 보상(Reward)이 시간에 상관없이 일정한 분포를 따른다고 가정한다. 그러나, 현실에서 그러한 경우는 거의 존재하지 않는다. 이 문제를 반영하여 만든 컨셉이 바로 Non-stationary bandits Problem이다.
-
Stationary Bandits: 보상에 대한 분포가 일정하다는 가정 하에서 문제를 풀어나간다. 따라서, 모든 파라미터들은 상수이며, 우리는 근사적으로라도 최선의 선택을 찾을 수 있다.
-
Non-stationary Bandits: 보상에 대한 분포가 일정하다는 가정이 존재하지 않는다. 따라서, 모든 파라미터들은 확률변수로 존재하며, 모든 시간에서의 최선의 옵션이란 존재하지 않는다.
Perspective on Non-stationary bandits
Non-stationary bandits problem를 바라보는 관점은 매우 다양하지만, 다음과 같이 크게 3가지로 나누어볼 수 있다.
- Adversarial bandits
매 iteration마다 player가 action을 선택하고, 상대방(adversary)가 그에 대한 보상(reward)를 정한다. 즉, (action,reward)의 값이 Random하게 선택된다.
성능이 매우 안좋을 것처럼 보이지만, 실제로 논문에선 Regret을 최소화하는 방법으로 의사 결정의 Randomizing을 제안하였다. 또한, 이 관점에선 분포에 대한 가정이 필요 없기 때문에, MAB문제에 대한 geteralized solution이라 볼 수 있다.
Regret= \[\left(\max_{i=1,\ldots,K} \mathbb E \sum_{t=1}^H x_{i,t}\right) - \mathbb E \sum_{t=1}^H x_{S_t,t}\]
-
contextual bandits
non-stationary bandits의 핵심은 environment에 따라 보상에 대한 분포가 변한다는 점이다. 여기서의 environment란 시간이 될 수도 있고, player에 대한 정보가 될 수도 있다. Contextual bandits에선 이 environment를 State라는 변수로 확장시켜 문제를 풀어나간다. 즉, action을 결정함에 있어서 과거의 reward값과 State를 동시에 고려한다.
여기서의 State는 MDP의 State와는 다르게 action에 따라 변화하지 않는다. -
stochastic bandits
보상에 대한 분포는 시간에 따라 stochastic하게 그려지며, 이 분포들은 각 arm에 대해 i.i.d하게 주어진다. Non-stationary 문제를 해결하기 위해선 여러 방법이 사용되지만, 대표적으론 각 시간마다 분포의 parameter를 다르게 지정하는 방법이 있다.
본 포스팅에선 Non-stationary stochastic bandits, 그 중에서도 Bayesian concept을 활용한 알고리즘에 대해 다룰 것이다.
Stochastic bandits
위에서도 언급했듯이 Stochastic bandits에선 시간 마다 분포의 parameter를 다르게 지정하여 Non-stationary 문제를 해결한다. 그렇다면 이 parameter들은 어떻게 다르게 지정할까?
각 arm지난 포스팅에서도 언급한 예시를 참고해보자. 이는 Stationary한 Thompson Sampling의 예시이다. 간단히 정리하자면 다음과 같다.
- beta분포의 parameter \(\alpha\)는 보상을 받은 횟수, \(\beta\)는 보상을 받지 않은 횟수로 지정된다.
- 지정된 파라미터를 바탕 생성한 분포에서 하나의 샘플을 뽑는다.
- 뽑은 샘플의 보상 기댓값을 계산하고, 이를 바탕으로 1번 방법과 같이 파라미터를 업데이트한다.
- 파라미터를 충분히 업데이트 하여 Posterior 분포를 구하고 최종 Action을 정한다.
위 예시에서의 Parameter는 계속 누적하여 더해지기 때문에, 과거 모든 action에 대한 정보를 담고 있다.
만약, 여기서 모든 과거의 action이 아닌 비교적 최근 action의 정보만 사용한다면 어떨까?
분포의 variation은 커지겠지만, 아마 시간 단위로 변화하는 reward의 특성을 더욱 잘 반영할 수 있을 것이다.
Stochastic bandits에선 이 컨셉을 적용하여 Non-stationary한 상황을 해결한다.
조금 더 구체적으로 말하자면, 과거 정보에 대한 영향을 줄이기 위해 discounting variable \(\gamma\)를 사용한다. 이는 시계열 자료분석에서도 자주 사용되는 exponential filtering의 개념과도 맞닿아 있다.
Dynamic Thompson Sampling
Dynamic TS는 exponential filtering의 개념을 Non-stationary 문제에 처음 도입한 알고리즘이다. 이 알고리즘에서는 기존 Thompson Sampling에 C라는 파라미터를 추가한다.
- C는 과거의 정보를 언제, 얼마나 discount할지 정하는 parameter이다.
자세한 알고리즘은 아래와 같다.
\(\theta_k\)는 k번째 arm의 성공확률로 brownian motion을 따른다.
\(\alpha\;+\;\beta\)는 한 interation 내에서의 지금까지의 시행 횟수이다.
-
만약 총 시행 횟수가 C보다 적다면, 기존 TS 알고리즘과 동일하게 Sample을 업데이트한다.
-
만약 총 시행 횟수가 C보다 크다면, 알고리즘은 과거 정보에 \(\frac{C}{C+1}\)만큼의 panelty를 준다.
논문에 따르면 위와 같은 식을 바탕으로 discount하는 과정은 exponential filtering의 식과 정확히 일치한다.
BUT,,,
이 알고리즘은 그 시점에서 play된 arm 에 대해서만 분포의 변화가 생긴다. 따라서, 시간에 따른 변화를 공평하게 적용하지 못한다는 단점이 있다.
이로 인해 발생할 수 있는 문제 중 하나는 과거 최적의 arm이 게임 중에 Stationary한 상태를 유지하고 local optima가 최적이 되는 경우이다. Dynamic TS는 과거 optimal arm의 통계적 특성이 변경되지 않고 있기 때문에 새로운 최적값으로 전환하기 어려우며, 따라서 다른 최적의 arm을 탐색할 기회가 사라지게 된다.
이를 보완한 모델이 아래 Discounted Thompson Sampling(DTS)이다.
Discounted Thompson Sampling
Discounted TS는 과거의 정보를 discount하여 반영한다는 점에서 Dynamic Thompson Sampling과 유사하나 다음에서 차이를 보인다.
- Posterior분포를 모든 시간에서 모든 arm에 대해 업데이트한다.
- 과거의 정보를 모든 timestep에서 discount하여 반영한다.
Notation
\(K\)={1,…,K} denotes the set of arms available to the decision maker
t: the time instant t \(\in\) {1,….,T}
\(X_{k,t}\): the reward obtained by the \(k^{th}\) arm at \(t^{th}\) time instant where \(X_{k,t}\)~Bernoulli(\(\theta\))
with mean \(\mu_{k,t}\) = E[\(X_{k,t}\)]
\(\mu^*\)=max[\(\mu_{k,t}\)] the best arm at instant t
\(\gamma\)= discounting factor\(\in\) (0,1]
\(\pi\): a candidate policy that selects an arm to pull during the game
\(\pi_t=\begin{cases}
\pi_1(U) & \text{ if } t=1 \\
\pi_t(U,X_{I_1^{\pi}},X_{I_2^{\pi}},…,X_{I_{t-1}^{\pi}})& \text{ if } t\geq 2
\end{cases}\)
regret: \(R^\pi(T)=\sum_{t=1}^{T}\mu_t^*-E_{\pi,\mu}[\sum_{t=1}^{T}X_{I_t^\pi,t}]\)
- 이 알고리즘에선 normalizing을 위해 \(\frac{1}{T}R^\pi(T)\)를 사용한다.
그렇다면 알고리즘을 자세히 살펴보자.
- \(S_I\)와 \(F_I\)는 현재 play된 arm, \(S_k\)와 \(F_k\)는 이번 time instant t에 play되지 않은 arm들의 parameter이다.
- 두가지 경우를 모두 업데이트하지만, 방법에 있어서는 차이를 보인다.
- \(\gamma\)= 1일 경우 traditional Thompson Sampling과 일치한다.
이 알고리즘은 어떤 장점이 있을까?
우리는 prior distribution의 parameter를 다음과 같이 정리할 수 있다.
그랗다면, 우리는 Prior분포의 기대값을 다음과 같이 표현할 수 있다.
이때, \(P(I_t^\pi=k)\)는 과거 정보를 바탕으로 arm k를 선택할 확률이다.
그렇다면, 선택하지 않은 arm의 경우는 어떻게 될까?
즉, play되지 않는 arm들의 평균은 constant하게 유지되지만, variance는 커진다. 이는 불확실한 arm에 대해exploration을 할 수 있도록 작동된다.
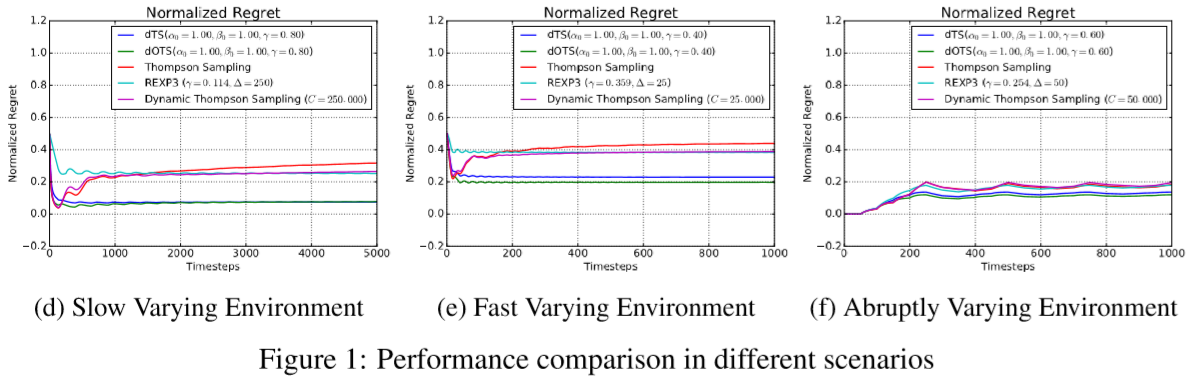
Performance
위와 같이 discounted TS가 좋은 성과를 보임을 알 수 있다.
Reference
TamingNon-stationaryBandits: ABayesianApproach
Thompsom Sampling for Dynamic Multi-armed Bandits